Materi Relasi dan Fungsi SMP terbaru
Adik adik yang sekarang masih di bangku SMP jika saat ini kalian sedang ingin belajar mengenai materi relasi dan fungsi maka artikel ini tepat untuk kalian. segera saja simak ya!
A.
Pengertian Relasi
Dalam kehidupan sehari – hari, banyak
kita temukan hubungan, misalnya hubungan pertemanan, hubungan pekerjaan,
hubungan kegemaran, dll.
Kata “ hubungan “ dapat digunakan
untuk menghubungkan dua (
himpunan ) dan hubungan tersebut memiliki sebuah “ nama “. Misalkan ada dua
kelompok, yaitu kelompok nama orang dan nama pekerjaan, lalu kedua kelompok
tersebut kita hubungkan dengan nama hubungan “ bekerja sebagai “, seperti
terlihat pada gambar berikut
Jadi, relasi dari himpunan A ke himpunan B adalah suatu aturan
yang memasangkan anggota anggota himpunan A dengan anggota – anggota
himpunan B
Contoh 1:
Misalkan ada dua himpunan A dan B dengan
A = í 1, 4, 9 ý
B = í 1, 2, 3,
4 ý
Relasi dari A ke B diberi nama kuadrat dari. Relasi
tersebut, digambarkan pada gambar berikut ini
A.
Menyatakan Relasi
Relasi antar dua himpunan dapat dinyatakan dengan 3
cara, yaitu :
1.
Diagram panah
2.
Diagram Cartesius
3.
Himpunan pasangan berurutan
Contoh :
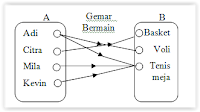
Diketahui himpunan anak A = íAdi, citra, Mila, Keviný dan
himpunan permainan
B = íBasket, Voli, Tenis meja ý Relasi
“Gemar bermain“
Nyatakan relasi dua hitungan itu dengan :
a.
Diagram panah
b.
Diagram Cartesius
c.
Himpunan pasangan berurutan
Jawab:
a. Diagram panah
b.
Diagram cartesius
c.
Himpunan pasangan
berurutan = í( Adi, Voli ), ( Adi, Tenis meja ), ( Citra, Basket ), ( Mila, Tenis meja), ( Kevin, Tenis meja ) ý
Latihan A dan B
1.
Buatlah diagram panah yang
menunjukkan relasi “ faktor dari “ dari himpunan K = í0, 1, 2ý ke himpunan L = í4, 5, 6ý
2.
Diketahui P = Q = í1, 2, 3, 4ý
a.
Buatlah diagram panah untuk
relasi “ faktor dari “ himpunan P ke himpunan Q!
b.
Nyatakan relasi tersebut
sebagai himpunan berurutan!
A.
Fungsi dan Pemetaan
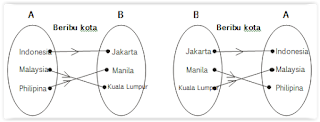
Perhatikan diagram panah berikut !
Setiap kota terletak pada satu propinsi, tidak ada kota
yang terletak pada beberapa propinsi
Pemetaan atau fungsi dari
himpunan A ke B adalah relasi khusus yang memasangkan setiap anggota
A dengan tepat satu anggota B
Contoh:
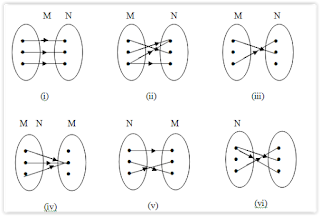
Nyatakan diagram - diagram panah berikut ini, apakah
pemetaan atau bukan ?
Jawab :
Gambar (i) bukan pemetaan, karena ada anggota A, yaitu b
yang memiliki lebih dari satu pasangan di B.
Gambar (ii) adalah pemetaan, karena masing-masing
anggota A memiliki tepat satu pasangan di B.
Gambar (iii) bukan pemetaan, karena
ada anggota A, yaitu b yang tidak memiliki pasangan di B.
Dari contoh-contoh diatas, ternyata
untuk mengetahui apakah suatu relasi merupakan pemetaan atau bukan, yang
terutama perlu diperhatikan adalah anggota-anggota himpunan A.
Berikut ini dibahas mengenai
istilah-istilah pada pemetaan. Perhatikan diagram pemetaan berikut
ini !
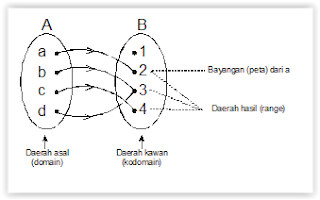
Perhatikan Gambar di atas!
P = {a, b, c,
d} disebut daerah asal (domain)
Q = {1, 2, 3, 4}
disebut daerah kawan (kodomain)
{2, 3, 4} disebut daerah hasil (range), yaitu himpunan
anggota-anggota Q yang mempunyai pasangan dengan anggota-anggota P.
a dipasangkan dengan 2, dapat ditulis a à 2, dibaca “ a dipetakan ke 2”
pada bentuk a à 2, 2 disebut
bayangan atau peta dari a.
Pemetaan adalah relasi khusus, maka
pemetaanpun dapat dinyatakan dengan diagram panah, diagram cartesius atau
himpunan pasangan berurutan.
Banyak pemetaan
dari dua himpunan
Diket:
A = {1, 2} dan B
= {3}
Dengan memperhatikan banyak anggota domain dan kodomain, banyak cara
pemetaan ditentukan dengan cara berikut:
Jika banyak anggota himpunan A = n(A)
Jika banyak anggota himpunan B = n(B)
Maka banyak, pemetaan dari A ke B adalah n(B)^n(A)
Contoh :
A = {a, b, c}
B = {1, 2 }
Banyak pemetaan dari A ke B =
= 23
= 8
D. Korespondensi
satu-satu
Perhatikan diagram panah berikut !
Setiap negara dipasangkan tepat satu dengan ibukotanya
dan setiap ibukota dipasangkan tepat satu dengan negaranya.
Himpunan A dikatakan berkorespondensi satu-satu dengan himpunan B jika setiap A
dipasangkan dengan tepat satu anggota B. Dan setiap anggota B dipasangkan tepat
satu anggota A. Dengan demikian, banyak
anggota himpunan A dan B haruslah sama.
Latihan C dan D
1.
Diagram panah berikut
menunjukkan relasi dari himpunan M ke himpunan N. Manakah yang merupakan
pemetaan dan manakah yang merupakan korespondensi satu-satu ?
1.
Setiap himpunan pasangan
berurutan berikut ini menunjukkan relasi dari himpunan A ke himpunan B. Relasi manakah
yang merupakan pemetaan?
a.
{(1,2), (2,2), (3,2)}
b.
{(a, 1), (b, 2), (b,3), (c, 4)}
c.
{(p, 1), (q, 2), (r, 1), (s,
2)}
2.
Berapakah banyak pemetaan yang
mungkin terjadi untuk pemetaan berikut!
a.
Dari himpunan K = {a, b, c, d}
ke himpunan L = {1,2,3}.
b.
Dari himpunan m = {p, q, r} ke
himpunan N = {1,2,3,4}
3.
Diantara pasangan – pasangan
himpunan berikut, manakah yang dapat berkorespondensi satu – satu?
a.
A = {0,2,4,6} dan B
= {1,2,5,7}
b.
Q = {warna
lampu lalu lintas}
c.
K = {huruf vokal}
dan
L = {hari dalam seminggu}
d.
M = {p,q,r,s}dan
N = {Faktor dari 8}
E. Menghitung Nilai Fungsi
Menghitung nilai suatu fungsi
berarti kita mengsubstitusi nilai variabel bebas ke dalam rumus fungsi sehingga
diperoleh variabel bergantungnya. Berikut ini diberikan beberapa contoh
menentukan nilai suatu fungsi.
Contoh 1
Pemetaan f : g ® R ditentukan oleh f (x) = 2 + x dengan G = {-1, 0, 1, 2, 3, 4} dan
R adalah himpunan bilangan real.
a.
Hitunglah f (3), f (0), dan f
(-1)
b.
Tentukan daerah hasil dari f
Jawab :
a.
f (3) = 2 + 3 = 5, f(0) = 2 + 0
= 2, dan f(-1) = 2 + (-1) = 1
b.
Dengan memasukkan setiap
anggota domain
G = {-1, 0,1,2,3,4}
ke dalam variabel bebas x pada rumus fungsi f(x) = 2 + x, mak diperoleh.
F(-1) = 1 f(1) = 3 f(3) = 5
F(0) = 2 f(2) = 4 f(4) = 6
Jadi, daerah hasil dari
f adalah {1,2,3,4,5,6}.
Contoh 2
Diketahui fungsi f : x ® 3x – 1. Tentukan :
a.
Rumus fungsi,
b.
Nilai fungsi untuk x = -3 dan x
= 2
Jawab :
F : x ® 3x -1
a. Rumus fungsi adalah f(x) = 3x – 1
b. Nilai fungsi untuk x = -3; f(-3) = 3
(-3) -1
= -9 -1
= -10
Nilai
fungsi untuk x = 2; f(2) = 3(2) – 1
= 5
Jadi, nilai fungsi untuk x = -3 adalah -10
dan untuk x = 2 adalah 5
Materi ini belum selesai karena keterbatasan tempat halaman. besok jika masih ada kesempatan akan dilanjut. semoga bermanfaat!
baca juga
|