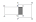Cara mudah menyelesaikan soal UN irisan bangun datar

Cara mudah menyelesaikan soal UN irisan bangun datar 

Kali ini kita akan khusus membahasa cara mudah menyelesaikan soal UN irisan bangun datar. Menjelaskan materi ini kepada siswa dan siswa bisa memahami dengan baik memang suatu tantangan tersendiri bagi pendidik. Berbagai masalah selalu timbul saat siswa diberikan penjelasan tenatang materi ini.

Pengalaman saya ketika mengajarkan soal UN irisan bangun datar  dengan menerapkan rumus yang biasanya di pakai mengalami kendala Jika tanpa di beri penjelasan yang baik. Sampai saya menemukan cara mudah menyelesaikan soal UN irisan bangun datar.

Misalkan saja soal UN irisan bangun datar nya seperti ini. Contoh ini kami ambil dari soal UN matematika SMP tahun 2012

1.        Perhatikan gambar persegi PQRS dengan PQ = 12 cm dan persegi panjang ABCD dengan DC = 15 cm, AD = 6 cm. 

Luas daerah yang tidak diarsir 198 cm², luas daerah yang diarsir adalah ....

A. 18 cm²

B. 36 cm²

C. 54 cm²

D. 72 cm²

Penyelesaian 

Luas yang diarsir adalah luas irisan dari bangun persegi panjang dan bangun persegi.

Untuk mencari luas irisan maka cara yang paling mudah untuk menyelesaikannya adalah dengan menggunakan rumus

Luas irisan = (Luas 1 + Luas 2 - Luas luar irisan)/2

Jadi soal diatas bisa dengan mudah diselesaikan seperti berikut ini.

Luas daerah yang diarsir = (luas ABCD + Luas PQRS - Luas yang tidak di arsir)/2

Luas daerah diarsir = (15 x 6 + 12x 12 - 198)/2 = (90 + 144 -198)/2 = 36/2 = 18 cm²

^{Bagaimana budah bukan?}

^{Kadang kadang soal yang keluar dalam ujian nasional adalah mencari luas daerah di luar irisan bangun. Maka untuk menyelesaikannya dapat digunakan rumus}

^{Luas luar irisan = Luas 1 + Luas 2 - 2 luas irisan}

^{yuk mari kita kaji cara mudah menyelesaikan soal UN irisan bangun datar pada contoh ke 2}

^{soal ini kami ambil dari soal UN 2016}

1.        Perhatikan gambar!

Luas daerah yang diarsir adalah ....

A. 297 cm²                  C. 243 cm²

B. 279 cm²                  D. 234 cm²

^Penjelasan 

^{Pada gambar diatas, Daerah yang merupakan irisan adalah segitiga AEC. Nah kadang jika guru tak memberikan penjelasan dulu maka siswa akan mengalami kesulitan dan memahami bahwa soal ini adalah soal irisan bangun datar dari dua segitiga yitu segitiga AEB dan segitiga AED dengan daerah segitiga AEC sebagai irisannya.}

Maka akan tampak bahwa luas daerah yang diarsir pada gambar di atas adalah luas daerah diluar irisan.

Jika begitu maka kita bisa menggunakan rumus

Luas arsiran = Luas AEB + Luas AED - 2 Luas AED

Luas daerah yang diarsir = (18x15)/2  + (18 x 24)/2 - 2 (18x6)/2

                                        = 135 + 216 - 108

                                        = 243 cm²

Bagaimana ternyata ada cara mudah dalam menyelesaikan soal UN irisan bangun datar.

Kadang soal ujian nasional memunculkan soal irisan dua lingkaran dengan variasinya. 

Untuk menyelesaikannya anda bisa baca artikel dibawah

cara mudah menyelesaikan masalah irisan dua lingkaran 

Semoga bermanfaat